La programación lineal es una técnica de optimización relativamente reciente, cuyo origen se remonta al desarrollo de herramientas para la ayuda a la toma de decisiones militares durante la Segunda Guerra Mundial. Se trata de un conjunto de procedimientos que permiten maximizar o minimizar una función objetivo, sujeta a un conjunto de restricciones lineales.
La sistematización de estos procedimientos y la demostración de su validez dentro de un marco de reglas y axiomas concretos, se debe al matemático estadounidense George B. Dantzig. En 1963 Dantzig publicó con la RAND Corporation (propiedad de las United States Air Forces) un completo manual acerca de la programación lineal titulado "Linear Programming and Extensions".
En este primer texto de programación lineal ya se identifican las primeras aplicaciones de la disciplina al campo metalúrgico: los problemas de mezclas en la carga metálica.
A continuación se desarrolla una variante del ejemplo 3-4 del manual de Dantzig para explicar la utilidad de esta disciplina.
El problema a resolver consiste en optimizar el coste de las materias primas utilizadas por una fundición para conseguir una aleación de composición 30% Ni, 30% Cr y 40% Fe.
En el mercado habrá disponibles materias primas de distinta composición a distinto precio. Tomemos por ejemplo la siguiente tabla de composiciones y precios para las fuentes de suministro A–I.
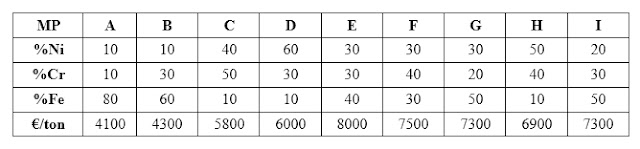 |
| Tabla de composiciones y precios para las fuentes de suministro A–I |
La fundición puede, por supuesto, comprar directamente al proveedor E, cuya materia prima coincide con la aleación objetivo, a 8000€/ton y despreocuparse de ajustar la composición del metal en el horno. A base de prueba y error se puede identificar que mezclando una cuarta parte de A y B con dos cuartas partes de H se obtiene el mismo resultado a un coste de 5550€/ton. Pero realizando más pruebas, se encuentra que este resultado es mejorable, ya que utilizando a partes iguales las materias primas A, B, C y D, se consigue la aleación objetivo por 5050€/ton. Sería posible encontrar la mezcla óptima, la más competitiva, con tan sólo calcular el coste de todas las posibles combinaciones de las fuentes de suministro y tomar aquella de menor precio.
Sin embargo, esto supondría realizar una cantidad ingente de cálculos para barrer todo el rango de posibles mezclas que dan lugar un 30% Ni, un 30% Cr y un 40% Fe. Es aquí donde entra en juego la programación lineal, ya que permite identificar la mezcla óptima en el menor número de pasos posible. Simplemente es necesario plantear la función de optimización y el conjunto de restricciones a cumplir, y aplicar el método Simplex desarrollado por Dantzig.
A continuación se explica cómo realizar el planteamiento, ya que abordar la aplicación del método Simplex, va más allá del alcance de este Blog.
Para plantear las ecuaciones que describen el problema de optimización, se tomarán las siguientes variables:
a = cantidad utilizada del suministro "A" para fabricar una tonelada de la aleación objetivo.
b = cantidad utilizada del suministro "B" para fabricar una tonelada de la aleación objetivo.
c = cantidad utilizada del suministro "C" para fabricar una tonelada de la aleación objetivo.
d = cantidad utilizada del suministro "D" para fabricar una tonelada de la aleación objetivo.
e = cantidad utilizada del suministro "E" para fabricar una tonelada de la aleación objetivo.
f = cantidad utilizada del suministro "F" para fabricar una tonelada de la aleación objetivo.
g = cantidad utilizada del suministro "G" para fabricar una tonelada de la aleación objetivo.
h = cantidad utilizada del suministro "H" para fabricar una tonelada de la aleación objetivo.
i = cantidad utilizada del suministro "I" para fabricar una tonelada de la aleación objetivo.
Con esta nomenclatura, la función de optimización objetivo "z" será:
4100a+4300b+5800c+600d+8000e+7500f+7300g+6900h+7300i = z (1)
que representa el precio de cada tonelada de mezcla resultante. El objetivo será por tanto minimizar “z”.
Las restricciones vendrán dadas por la obligación de cumplir con un 30% de Ni, un 30% Cr y un 40% de Fe en la carga del horno y serán, por tanto, expresadas como tres ecuaciones:
10a+10b+40c+60d+30e+30f+30g+50h+20i=30 (2)
10a+30b+50c+30d+30e+40f+20g+40h+30i=30 (3)
80a+60b+10c+10d+40e+30f+50g+10h+50i=40 (4)
Existen además dos restricciones que se consideran implícitas, pero que conviene explicitar:
- No se puede comprar una cantidad negativa de materia prima:
a≥0; b≥0; c≥0; d≥0; e≥0; f≥0; g≥0; h≥0; i≥0 (5)
- La suma de las fracciones utilizadas de cada proveedor debe dar lugar al 100% de una tonelada:
a+b+c+d+e+f+g+h+i=1 (6)
La aplicación del método Simplex al sistema (1) (2) (3) (4) (5) (6) da lugar a una solución óptima de coste 4980 €/ton, con una mezcla compuesta por tres quintas partes de B y dos quintas partes de D, sabiendo además que no existe otra solución más rentable.
Con la esperanza de que este ejemplo concreto haya despertado la curiosidad del lector acerca de las distintas técnicas de optimización que utiliza Ik4-Azterlan para reforzar la competitividad del sector metalúrgico, nos despedimos hasta el próximo post de matemáticas para la metalurgia.

No hay comentarios:
Publicar un comentario